
Perspective Projection on the Computer
Perspective Projection on the Computer
Perspective projection is a means of representing something that is three-dimensional in a two-dimensional space, or in other words the representation of 3D in 2D, something we are all familiar with from the computer of course and also TV, photographs, paintings and drawings.
A basic rule of perspective projection is that something that is further away from the viewer at a three-dimensional space is ???smaller??? in the two-dimensional representation and ???larger??? if it is closer.
 This holds true even for seemingly two-dimensional objects in the 3D world, like a flat painting from the front. Now everything in the real world is three-dimensional, but some things do not appear that way, or at least not much, to the human eye. If one dimension is too small, an object will appear two-dimensional to us.
This holds true even for seemingly two-dimensional objects in the 3D world, like a flat painting from the front. Now everything in the real world is three-dimensional, but some things do not appear that way, or at least not much, to the human eye. If one dimension is too small, an object will appear two-dimensional to us.
Axonometric Projection
If the object is really ???thick??? or ???deep??? or we know from experience that the object is that way, a representation of the object in 2D is enhanced if not only one side (or two dimensions) are shown, the width and the height, but also the part of the side that we determine as the ???depth???. Axonometric projection is the term used in geometry to describe the representation of an object with two or more ???sides??? visible to get a feeling of its width, height and depth.
There are three main sub forms of axonometric projection, which are isometric, dimetric and trimetric projection. The difference between the three is the angle and perspective of the viewer to the object.
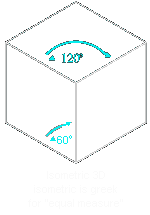 In isometric projection for example, the angles between the projection of the x, y, and z-axes are the same or 120-degrese.
In isometric projection for example, the angles between the projection of the x, y, and z-axes are the same or 120-degrese.
In dimetric-projection, only two of the three axes in space must be foreshortened equally, while the angle and scale of the third axis can vary.
If all three axes appear to be foreshortened differently, we talk about trimetric projection.
 Short summary
Short summary
Isometric = angles for x, y, z are the same, dimetric = only two are the same, trimetric = none is the same. See the illustration that shows an example for each type of projection.
Each of those types of projections were a pain and difficult to master for early computer generations, because the math behind them is very complex.
The Cheat: Oblique-Projection
Early computer generations used often oblique-projection for simple 3D effects, because it was relatively easy to do.
One way to draw using oblique-projection is to draw the side of the object you are looking at in two dimensions, i.e. flat. Then draw the other side???s at an angle of 45 degrees, but instead of drawing the sides full size, you only draw them with half the depth. This 45-degree angle was easy to manage.
Think about a computer screen as something like a checkerboard and draw an imaginable square on it. To draw the third dimension lines, you simply start at a corner, go one square to the side and then one square up or down, depending on the angle. You repeat this until you marked the number of squares that represent half of the actual length of that side. Drawing a proper line if the angle is different from 45-degrees becomes difficult. See the illustration that shows lines at different angles on a computer (click on the image to enlarge it).
The beauty with the simple 45-degrees oblique projection was that you do not have to do any vector calculations. Vector calculations take up CPU time (a lot, because of the needed divisions and work with floating points, something older computers were unable to deal with), nor did you require sophisticated line drawing algorithms like the famous Bresenham algorithm.
 The Commodore 64 for example did not have a floating-point unit. The C-64 CPU was not able to do any kind of floating point operations, which was the reason why real-time 3D-animation did not exist on this machine (until much later, when smart coders used tricks to work around that problem to create visual effects that look like 3D vector graphics.
The Commodore 64 for example did not have a floating-point unit. The C-64 CPU was not able to do any kind of floating point operations, which was the reason why real-time 3D-animation did not exist on this machine (until much later, when smart coders used tricks to work around that problem to create visual effects that look like 3D vector graphics.
Seeing Pixels? Missed the Anti Aliasing, eh?
Even if you got the stuff calculated and the basic lines drawn was there still a problem. If you draw a line that is not 45deg on a computer screen pixel will become visible badly (the Bresenham article shows it nicely). In order to compensate for this side effect had to be used another, even more complicated method be used, which is generally known as anti-aliasing.
Anti aliasing is a trick for the human-eye, which makes sharp edges appear blurry and if done very well even soft. If this is combined with motion (what is even harder to do), the human eye will not notice this blurriness anymore and the edges will appear clean and sharp as they did when it was a simple 45deg angle.
It is more challenging if the angle is anything else but 45-degrees, for the programmer who tries to get a 3D-object on the 2D screen and also for the artist who tries to do the same thing with a single picture.
Thanks God for FPU and Photoshop
Computers became more powerful and most home computers today have 3D acceleration build into their graphics card in addition to one or more powerful CPU with special floating-point calculation unit. The artists got help too. Modern graphical applications provide build-in features for anti-aliasing. This was done by hand in the past.
Anti-Aliasing by Hand Have a look at the famous ???Fairlight??? logo pixeled by Angel Dawn on the Commodore Amiga in a resolution of 320×256 and only 32 colors. There were no build-in features for anti-aliasing back then. The artist had to do it himself by setting additional pixels with the right color next to the pixels of the actual line. I enlarged one corner of the logo that you can see how he did it. Remarkable, isn???t it?
Have a look at the famous ???Fairlight??? logo pixeled by Angel Dawn on the Commodore Amiga in a resolution of 320×256 and only 32 colors. There were no build-in features for anti-aliasing back then. The artist had to do it himself by setting additional pixels with the right color next to the pixels of the actual line. I enlarged one corner of the logo that you can see how he did it. Remarkable, isn???t it?
For additional and even more remarkable example of hand done anti-aliasing and pixeling, check out my post about the art by Dream Design from last summer. Yes, believe it or not, all of the images were hand pixeled. No Photoshop was used and no, those are not digital or scanned photographs either.
Cheers!
Carsten aka Roy/SAC
 Posted on: Monday, October 22nd, 2007 02:54
Posted on: Monday, October 22nd, 2007 02:54






I think each of those types of projections were a pain and difficult to master for early computer generations, because the math behind them is very complex.
No doubt about that. It’s even hard for a human to do manually and get it right, imagine what it takes to come up with some fast and working routines that can do this kind of stuff automatically.